Comparison: Mandala vs Sommer

Side-by-side analysis for quantitative genetics applications

Overview

This tutorial compares the mandala package with the popular sommer package for analyzing agricultural field trials. Both packages are designed for mixed model analysis but have different strengths and use cases.

What you’ll learn

Key differences between Mandala and Sommer
Side-by-side analysis of the same datasets
Variance component estimation comparison
Heritability calculation methods
When to use each package

Background

Sommer Package

Purpose: Solving mixed model equations in plant breeding and genetics
Key Features:
- Multivariate models
- Genomic selection models (GBLUP)
- AI-REML algorithm
- Custom relationship matrices
Primary Use: Quantitative genetics, genomic prediction

Mandala Package

Purpose: Agricultural field trial analysis
Key Features:
- Streamlined workflow for standard designs
- Built-in spatial analysis
- User-friendly interface
- Unified heritability estimation
Primary Use: Field trial analysis, variety testing

Loading Packages

# library(mandala)  # Install Mandala first (request download: https://listoagriculture.com/products)
library(sommer)
library(dplyr)
library(ggplot2)
library(tidyr)

Example 1: Simple RCBD

Data Setup

We’ll simulate data with known variance components to validate both approaches:

set.seed(123)
n_genotypes <- 15
n_blocks <- 4

rcbd_data <- expand.grid(
  genotype = factor(paste0("G", sprintf("%02d", 1:n_genotypes))),
  block = factor(paste0("B", 1:n_blocks))
)

# True variance components (for validation)
true_gen_var <- 400
true_block_var <- 100
true_error_var <- 300

# Simulate yield
genotype_effects <- rnorm(n_genotypes, 0, sqrt(true_gen_var))
block_effects <- rnorm(n_blocks, 0, sqrt(true_block_var))

rcbd_data$yield <- 5000 +
  genotype_effects[as.numeric(rcbd_data$genotype)] +
  block_effects[as.numeric(rcbd_data$block)] +
  rnorm(nrow(rcbd_data), 0, sqrt(true_error_var))

head(rcbd_data)

  genotype block    yield
1      G01    B1 4998.471
2      G02    B1 4994.770
3      G03    B1 5045.268
4      G04    B1 5001.508
5      G05    B1 5007.830
6      G06    B1 5041.344

True Variance Components

Genotype variance: 400
Block variance: 100
Error variance: 300

Analysis with Mandala

#-----------------------------------
# RCBD with Mandala
#-----------------------------------

# Fit model (genotype fixed, block random)
mandala_fixed <- mandala(
  fixed  = yield ~ genotype,
  random = ~ block,
  data   = rcbd_data
)

# View variance components
mandala_vc <- summary(mandala_fixed)$varcomp
print(mandala_vc)

# For heritability: fit genotype as random
mandala_random <- mandala(
  fixed  = yield ~ 1,
  random = ~ genotype + block,
  data   = rcbd_data
)

# Unified heritability estimates
h2 <- h2_estimates(
  random_mod = mandala_random,
  fixed_mod  = mandala_fixed,
  genotype   = "genotype"
)
print(h2)

# Extract BLUEs
blues <- mandala_fixed$BLUEs
head(blues)

Analysis with Sommer

# Fit model with sommer (genotypes as random for variance estimation)
sommer_model <- mmer(
  fixed = yield ~ 1,
  random = ~ genotype + block,
  data = rcbd_data,
  verbose = FALSE
)

# Extract variance components
sommer_vc <- summary(sommer_model)$varcomp
print("Sommer Variance Components:")

[1] "Sommer Variance Components:"

print(sommer_vc)

                      VarComp VarCompSE   Zratio Constraint
genotype.yield-yield 341.3026 158.12626 2.158418   Positive
block.yield-yield    191.0388 172.26593 1.108976   Positive
units.yield-yield    300.7722  65.65848 4.580858   Positive

# Calculate heritability
var_g <- sommer_vc["genotype", "VarComp"]
var_e <- sommer_vc["units", "VarComp"]
h2_sommer <- var_g / (var_g + var_e / n_blocks)
cat("\nSommer Heritability (entry-mean basis):", round(h2_sommer, 3), "\n")


Sommer Heritability (entry-mean basis): 0.819

# Extract BLUPs
blups <- randef(sommer_model)$genotype
head(blups)

NULL

Example 2: Multi-Environment Trial

Data Setup

set.seed(456)
n_genotypes <- 20
n_envs <- 3
n_blocks <- 3

met_data <- expand.grid(
  genotype = factor(paste0("G", sprintf("%02d", 1:n_genotypes))),
  env = factor(paste0("E", 1:n_envs)),
  block = factor(paste0("B", 1:n_blocks))
)

# True variance components
true_var_g <- 500
true_var_gxe <- 200
true_var_error <- 400

# Simulate
met_data$yield <- 6000 +
  rnorm(n_genotypes, 0, sqrt(true_var_g))[as.numeric(met_data$genotype)] +
  rnorm(n_envs, 0, 300)[as.numeric(met_data$env)]

# Add GxE
gxe <- matrix(rnorm(n_genotypes * n_envs, 0, sqrt(true_var_gxe)), 
              n_genotypes, n_envs)
met_data$yield <- met_data$yield + 
  gxe[cbind(as.numeric(met_data$genotype), as.numeric(met_data$env))]

# Add block(env) and error
met_data$env_block <- factor(paste0(met_data$env, "_", met_data$block))
met_data$yield <- met_data$yield + 
  rnorm(n_envs * n_blocks, 0, 50)[as.numeric(met_data$env_block)] +
  rnorm(nrow(met_data), 0, sqrt(true_var_error))

head(met_data)

  genotype env block    yield env_block
1      G01  E1    B1 5861.335     E1_B1
2      G02  E1    B1 5902.917     E1_B1
3      G03  E1    B1 5880.556     E1_B1
4      G04  E1    B1 5822.048     E1_B1
5      G05  E1    B1 5856.848     E1_B1
6      G06  E1    B1 5885.062     E1_B1

Sommer MET Analysis

sommer_met <- mmer(
  fixed  = yield ~ env,
  random = ~ genotype + genotype:env + env:block,
  data   = met_data,
  verbose = FALSE
)

# Variance components
met_vc <- summary(sommer_met)$varcomp
print("Sommer MET Variance Components:")

[1] "Sommer MET Variance Components:"

print(met_vc)

                           VarComp VarCompSE   Zratio Constraint
genotype.yield-yield      500.1213 192.74417 2.594742   Positive
genotype:env.yield-yield  127.6429  65.18364 1.958205   Positive
env:block.yield-yield    1347.2640 790.20255 1.704960   Positive
units.yield-yield         432.1280  57.23833 7.549626   Positive

# Extract components
var_g <- met_vc["genotype", "VarComp"]
var_gxe <- met_vc["genotype:env", "VarComp"]
var_e <- met_vc["units", "VarComp"]

# Entry-mean heritability across environments
h2_met <- var_g / (var_g + var_gxe/n_envs + var_e/(n_envs * n_blocks))
cat("\nEntry-mean heritability:", round(h2_met, 3), "\n")


Entry-mean heritability: NA

Example 3: Spatial Analysis

set.seed(789)
n_rows <- 10
n_cols <- 10

spatial_data <- data.frame(
  row = rep(1:n_rows, each = n_cols),
  col = rep(1:n_cols, times = n_rows),
  genotype = factor(sample(paste0("G", 1:25), n_rows * n_cols, replace = TRUE))
)

# Add spatial trend + genotype effects + error
gen_eff <- setNames(rnorm(25, 0, 300), paste0("G", 1:25))
spatial_data$yield <- 5000 + 
  gen_eff[spatial_data$genotype] +
  30 * spatial_data$row - 20 * spatial_data$col +
  rnorm(nrow(spatial_data), 0, 200)

Visualize Field Pattern

ggplot(spatial_data, aes(x = col, y = row, fill = yield)) +
  geom_tile() +
  scale_fill_gradient2(low = "#2E6B8A", mid = "#FAF8F5", high = "#9B5B5B",
                       midpoint = mean(spatial_data$yield)) +
  coord_equal() +
  theme_minimal() +
  labs(title = "Field Map - Spatial Trend Visible",
       x = "Column", y = "Row")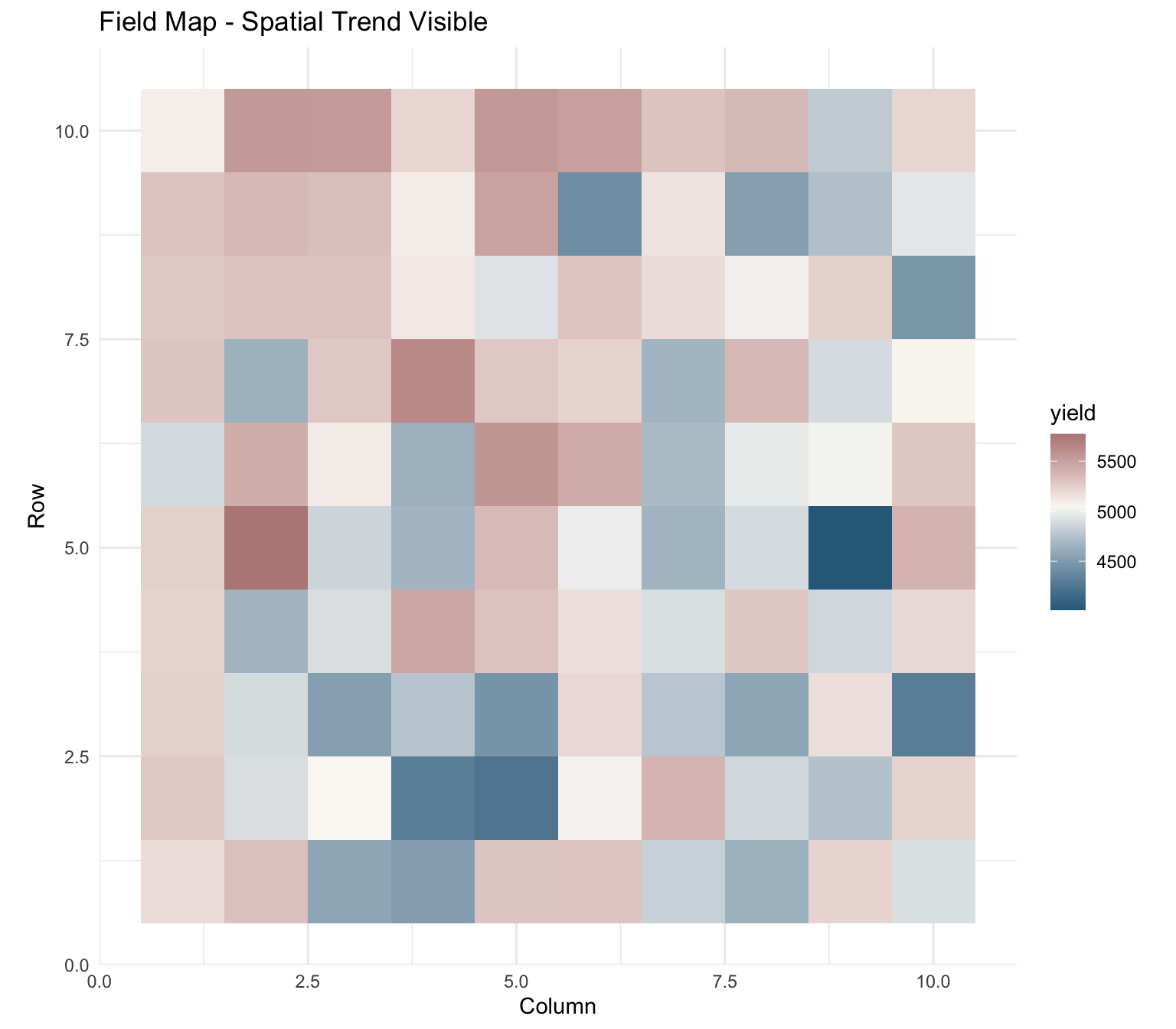

Sommer with Row-Column Effects

spatial_data$row_f <- factor(spatial_data$row)
spatial_data$col_f <- factor(spatial_data$col)

sommer_spatial <- mmer(
  fixed = yield ~ 1,
  random = ~ genotype + row_f + col_f,
  data = spatial_data,
  verbose = FALSE
)

print(summary(sommer_spatial)$varcomp)

                        VarComp VarCompSE    Zratio Constraint
genotype.yield-yield 62242.1591 22296.159 2.7916091   Positive
row_f.yield-yield    11391.4155  8201.081 1.3890139   Positive
col_f.yield-yield      490.7583  3227.847 0.1520389   Positive
units.yield-yield    47209.7972  8710.007 5.4201793   Positive

Key Differences Summary

Aspect	Mandala	Sommer
Syntax	Simple formula interface	More verbose
Heritability	Built-in `h2_estimates()`	Manual calculation
Spatial models	Built-in AR1 structures	Via custom covariance
Genomic models	Limited	Extensive (GBLUP, etc.)
Multivariate	No	Yes
Speed	Fast	Moderate

When to Use Each

Use Mandala when:

Standard field trial designs
Need spatial correlation modeling
Routine variety testing
Quick heritability estimates

Use Sommer when:

Genomic prediction (GBLUP)
Multi-trait analysis
Custom relationship matrices
Complex variance structures

Additional Resources

Sommer: https://cran.r-project.org/package=sommer
Mandala: https://listoagriculture.com/products

Session Information

sessionInfo()

R version 4.5.2 (2025-10-31)
Platform: aarch64-apple-darwin20
Running under: macOS Tahoe 26.1

Matrix products: default
BLAS:   /System/Library/Frameworks/Accelerate.framework/Versions/A/Frameworks/vecLib.framework/Versions/A/libBLAS.dylib 
LAPACK: /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRlapack.dylib;  LAPACK version 3.12.1

locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8

time zone: America/New_York
tzcode source: internal

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods   base     

other attached packages:
[1] tidyr_1.3.1    ggplot2_4.0.0  dplyr_1.1.4    sommer_4.4.4   enhancer_1.1.0
[6] crayon_1.5.3   MASS_7.3-65    Matrix_1.7-4  

loaded via a namespace (and not attached):
 [1] gtable_0.3.6       jsonlite_2.0.0     compiler_4.5.2     tidyselect_1.2.1  
 [5] Rcpp_1.1.0         scales_1.4.0       yaml_2.3.10        fastmap_1.2.0     
 [9] lattice_0.22-7     R6_2.6.1           labeling_0.4.3     generics_0.1.4    
[13] knitr_1.50         htmlwidgets_1.6.4  tibble_3.3.0       pillar_1.11.1     
[17] RColorBrewer_1.1-3 rlang_1.1.6        xfun_0.54          S7_0.2.0          
[21] cli_3.6.5          withr_3.0.2        magrittr_2.0.4     digest_0.6.37     
[25] grid_4.5.2         lifecycle_1.0.4    vctrs_0.6.5        evaluate_1.0.5    
[29] glue_1.8.0         farver_2.1.2       rmarkdown_2.30     purrr_1.1.0       
[33] tools_4.5.2        pkgconfig_2.0.3    htmltools_0.5.8.1