Working with Example Datasets

Analyzing common experimental designs with Mandala

Overview

This tutorial demonstrates how to analyze real agricultural field trial datasets using the mandala package. We’ll work with common experimental designs and show how to properly specify models.

Loading Packages

# library(mandala)  # Install Mandala first (request download: https://listoagriculture.com/products)
library(dplyr)
library(ggplot2)
library(tidyr)

Dataset 1: Randomized Complete Block Design (RCBD)

Data Description

A typical RCBD experiment with:

20 genotypes
3 replications (blocks)
Response: grain yield (kg/ha)

# Create realistic RCBD dataset
set.seed(456)
n_genotypes <- 20
n_blocks <- 3

rcbd_data <- expand.grid(
  genotype = factor(paste0("G", 1:n_genotypes)),
  block = factor(paste0("B", 1:n_blocks))
)

# Simulate realistic yield data
rcbd_data$yield <- 5000

# Add genotype effects (some good, some poor yielders)
genotype_effects <- c(
  rnorm(5, mean = 800, sd = 100),   # High yielders
  rnorm(10, mean = 0, sd = 150),    # Average yielders
  rnorm(5, mean = -600, sd = 100)   # Low yielders
)
rcbd_data$yield <- rcbd_data$yield + 
  genotype_effects[as.numeric(rcbd_data$genotype)]

# Add block effects
block_effects <- c(200, -100, -50)
rcbd_data$yield <- rcbd_data$yield + 
  block_effects[as.numeric(rcbd_data$block)]

# Add error term
rcbd_data$yield <- rcbd_data$yield + rnorm(nrow(rcbd_data), mean = 0, sd = 300)

head(rcbd_data, 10)

   genotype block    yield
1        G1    B1 5723.267
2        G2    B1 4881.472
3        G3    B1 5020.040
4        G4    B1 5046.350
5        G5    B1 4783.985
6        G6    B1 5113.979
7        G7    B1 4499.892
8        G8    B1 4729.488
9        G9    B1 5199.150
10      G10    B1 5735.364

Exploratory Data Analysis

# Summary statistics by genotype
rcbd_summary <- rcbd_data %>%
  group_by(genotype) %>%
  summarise(
    mean_yield = mean(yield),
    sd_yield = sd(yield),
    cv = (sd_yield / mean_yield) * 100
  ) %>%
  arrange(desc(mean_yield))

head(rcbd_summary, 10)

# A tibble: 10 × 4
   genotype mean_yield sd_yield    cv
   <fct>         <dbl>    <dbl> <dbl>
 1 G11           5760.    171.   2.97
 2 G10           5734.    152.   2.65
 3 G12           5589.     99.8  1.79
 4 G13           5441.    349.   6.41
 5 G1            5406.    413.   7.64
 6 G16           5336.    389.   7.29
 7 G20           5241.     87.5  1.67
 8 G14           5232.    107.   2.05
 9 G15           5197.    154.   2.96
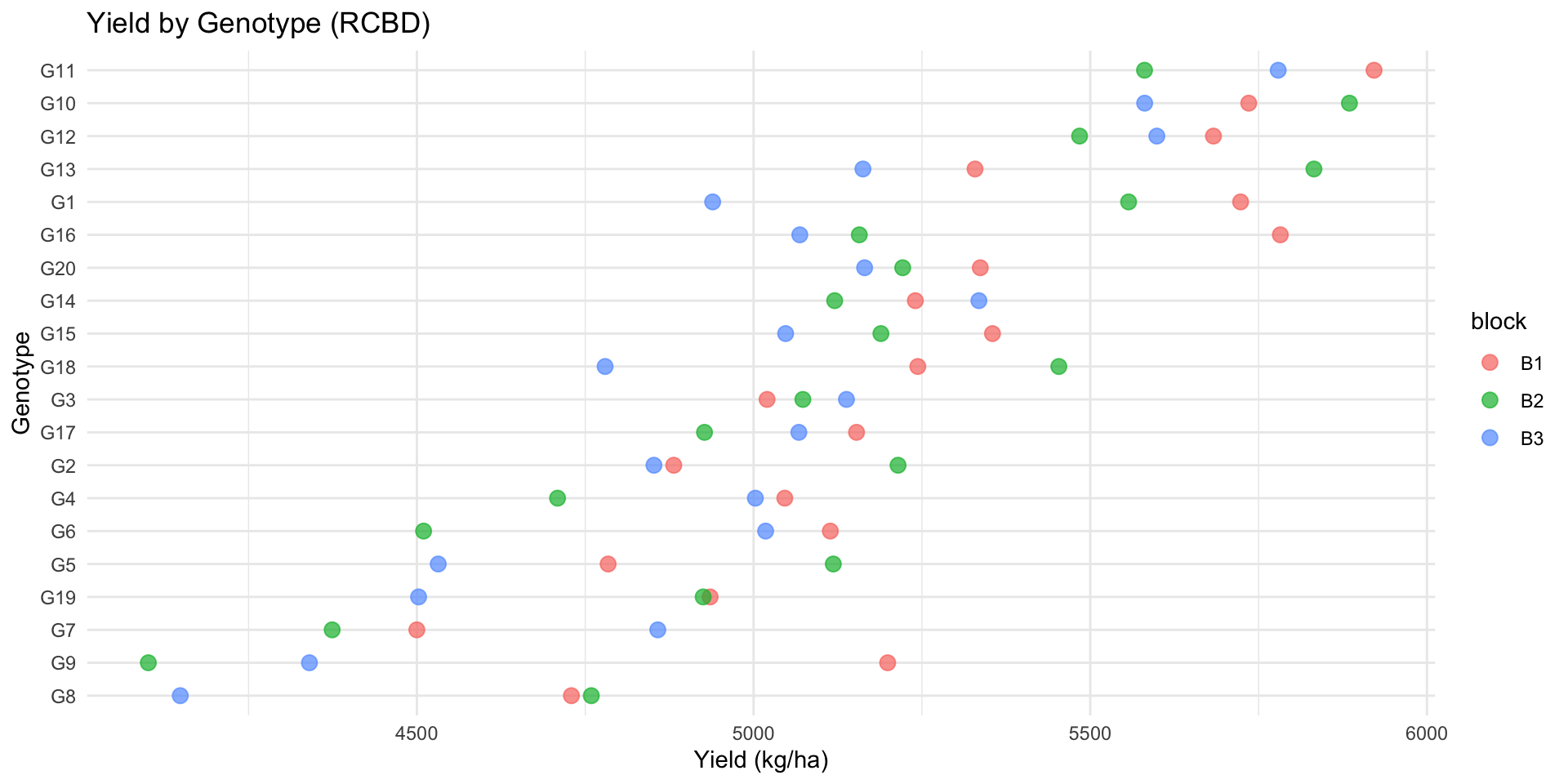
10 G18           5159.    345.   6.68

# Visualization
ggplot(rcbd_data, aes(x = reorder(genotype, yield), y = yield, color = block)) +
  geom_point(size = 3, alpha = 0.7) +
  coord_flip() +
  theme_minimal() +
  labs(
    title = "Yield by Genotype (RCBD)",
    x = "Genotype", 
    y = "Yield (kg/ha)"
  )

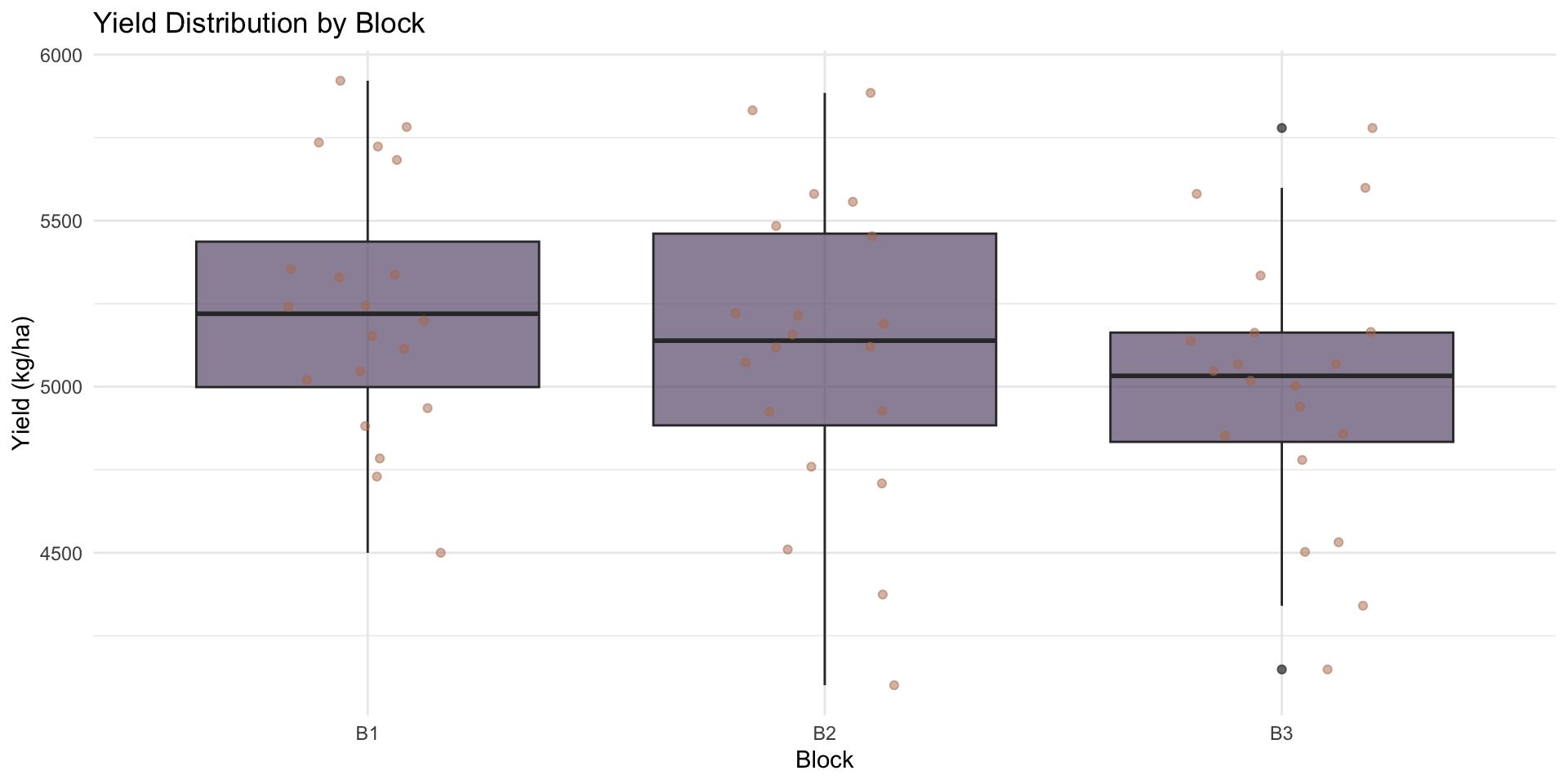
# Block effects
ggplot(rcbd_data, aes(x = block, y = yield)) +
  geom_boxplot(fill = "#6B5A7D", alpha = 0.7) +
  geom_jitter(width = 0.2, alpha = 0.5, color = "#B5795A") +
  theme_minimal() +
  labs(
    title = "Yield Distribution by Block",
    x = "Block", 
    y = "Yield (kg/ha)"
  )

Model Fitting with Mandala

# Fit the RCBD model
rcbd_model <- mandala(
  fixed  = yield ~ genotype,
  random = ~ block,
  data   = rcbd_data
)

# View model summary and variance components
summary(rcbd_model)

# Extract variance components table
var_components <- summary(rcbd_model)$varcomp
print(var_components)

# Heritability Estimation
rcbd_model_rand <- mandala(
  fixed  = yield ~ 1,
  random = ~ genotype + block,
  data   = rcbd_data
)

h2_table <- h2_estimates(
  random_mod = rcbd_model_rand,
  fixed_mod  = rcbd_model,
  genotype   = "genotype"
)
print(h2_table)

# Extract BLUEs and Rank Genotypes
blues <- rcbd_model$BLUEs
genotype_ranking <- blues %>% arrange(desc(estimate))
print(genotype_ranking)

Dataset 2: Alpha-Lattice Design

Data Description

An alpha-lattice design with:

50 genotypes
2 replications
Incomplete blocks of size 5 within each replication

set.seed(789)
n_genotypes <- 50
n_reps <- 2
block_size <- 5
n_blocks_per_rep <- n_genotypes / block_size

# Create design structure
alpha_data <- data.frame(
  genotype = factor(rep(paste0("G", 1:n_genotypes), times = n_reps)),
  rep = factor(rep(1:n_reps, each = n_genotypes))
)

# Assign incomplete blocks within reps
alpha_data$incomplete_block <- factor(
  paste0(alpha_data$rep, ".", 
         rep(rep(1:n_blocks_per_rep, each = block_size), times = n_reps))
)

# Simulate yield data
alpha_data$yield <- 6000

# Add genotype effects
genotype_effects <- rnorm(n_genotypes, mean = 0, sd = 400)
alpha_data$yield <- alpha_data$yield + 
  genotype_effects[as.numeric(alpha_data$genotype)]

# Add rep effects
rep_effects <- c(300, -300)
alpha_data$yield <- alpha_data$yield + 
  rep_effects[as.numeric(alpha_data$rep)]

# Add incomplete block effects
n_incomplete_blocks <- n_reps * n_blocks_per_rep
incomplete_block_effects <- rnorm(n_incomplete_blocks, mean = 0, sd = 200)
alpha_data$yield <- alpha_data$yield + 
  incomplete_block_effects[as.numeric(alpha_data$incomplete_block)]

# Add error
alpha_data$yield <- alpha_data$yield + rnorm(nrow(alpha_data), mean = 0, sd = 350)

head(alpha_data, 10)

   genotype rep incomplete_block    yield
1        G1   1              1.1 6690.737
2        G2   1              1.1 6256.748
3        G3   1              1.1 6364.876
4        G4   1              1.1 6398.428
5        G5   1              1.1 6426.309
6        G6   1              1.2 5131.415
7        G7   1              1.2 7174.288
8        G8   1              1.2 6985.033
9        G9   1              1.2 6968.603
10      G10   1              1.2 4985.144

Model Fitting

# Fit Alpha-Lattice Model
alpha_model_fixed <- mandala(
  fixed  = yield ~ genotype,
  random = ~ rep + rep:incomplete_block,
  data   = alpha_data
)

summary(alpha_model_fixed)
var_comps_alpha <- summary(alpha_model_fixed)$varcomp
print(var_comps_alpha)

# Heritability Estimation
alpha_model_random <- mandala(
  fixed  = yield ~ 1,
  random = ~ genotype + rep + rep:incomplete_block,
  data   = alpha_data
)

h2_alpha <- h2_estimates(
  random_mod = alpha_model_random,
  fixed_mod  = alpha_model_fixed,
  genotype   = "genotype"
)
print(h2_alpha)

# BLUPs
blups_alpha <- mandala_predict(alpha_model_random, classify_term = "genotype")
head(blups_alpha)

Dataset 3: Multi-Environment Trial

Data Description

A multi-environment trial with:

30 genotypes
4 locations (environments)
3 blocks per location

set.seed(101)
n_genotypes <- 30
n_locations <- 4
n_blocks <- 3

met_data <- expand.grid(
  genotype = factor(paste0("G", 1:n_genotypes)),
  location = factor(paste0("Loc", 1:n_locations)),
  block = factor(paste0("B", 1:n_blocks))
)

# Simulate yield data
met_data$yield <- 5500

# Add genotype main effects
genotype_effects <- rnorm(n_genotypes, mean = 0, sd = 300)
met_data$yield <- met_data$yield + 
  genotype_effects[as.numeric(met_data$genotype)]

# Add location effects
location_effects <- c(800, 200, -300, -700)
met_data$yield <- met_data$yield + 
  location_effects[as.numeric(met_data$location)]

# Add genotype x location interaction
gxe_effects <- matrix(
  rnorm(n_genotypes * n_locations, mean = 0, sd = 250), 
  nrow = n_genotypes, 
  ncol = n_locations
)
met_data$yield <- met_data$yield + 
  gxe_effects[cbind(as.numeric(met_data$genotype), 
                    as.numeric(met_data$location))]

# Add block within location effects
n_block_loc <- n_locations * n_blocks
block_loc_effects <- rnorm(n_block_loc, mean = 0, sd = 150)
met_data$block_loc <- factor(paste0(met_data$location, "_", met_data$block))
met_data$yield <- met_data$yield + 
  block_loc_effects[as.numeric(met_data$block_loc)]

# Add error
met_data$yield <- met_data$yield + rnorm(nrow(met_data), mean = 0, sd = 400)

head(met_data, 10)

   genotype location block    yield block_loc
1        G1     Loc1    B1 5731.465   Loc1_B1
2        G2     Loc1    B1 5523.519   Loc1_B1
3        G3     Loc1    B1 5900.409   Loc1_B1
4        G4     Loc1    B1 6928.250   Loc1_B1
5        G5     Loc1    B1 5208.988   Loc1_B1
6        G6     Loc1    B1 5877.214   Loc1_B1
7        G7     Loc1    B1 6453.261   Loc1_B1
8        G8     Loc1    B1 5900.387   Loc1_B1
9        G9     Loc1    B1 6430.253   Loc1_B1
10      G10     Loc1    B1 6269.523   Loc1_B1

Exploratory Analysis

# Location summary
met_data %>%
  group_by(location) %>%
  summarise(
    mean_yield = mean(yield),
    sd_yield = sd(yield),
    min_yield = min(yield),
    max_yield = max(yield)
  )

# A tibble: 4 × 5
  location mean_yield sd_yield min_yield max_yield
  <fct>         <dbl>    <dbl>     <dbl>     <dbl>
1 Loc1          6156.     488.     4924.     7290.
2 Loc2          5567.     605.     4126.     6960.
3 Loc3          5304.     536.     4058.     6528.
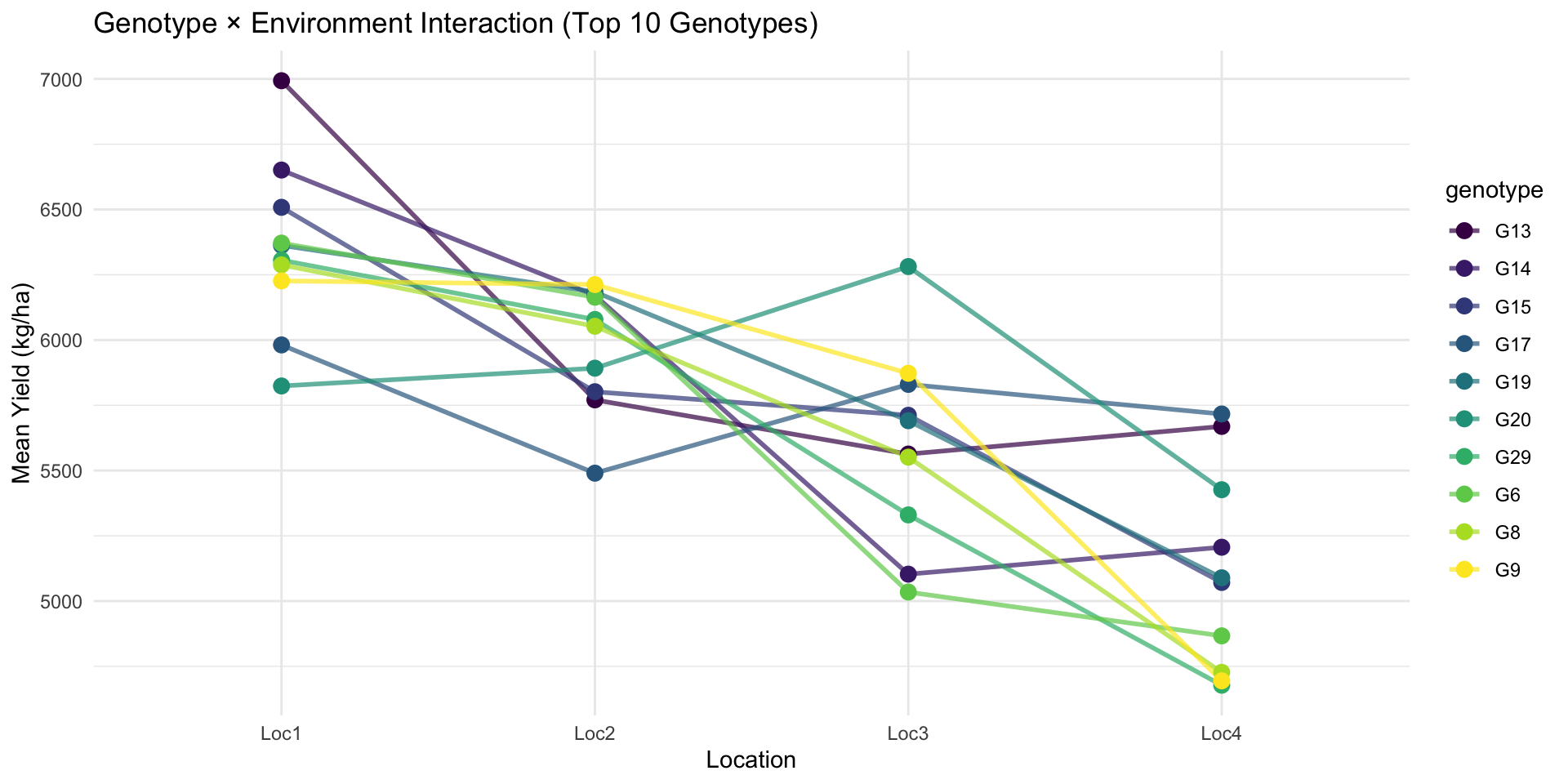
4 Loc4          4686.     545.     3584.     6042.

# GxE interaction plot
met_means <- met_data %>%
  group_by(genotype, location) %>%
  summarise(mean_yield = mean(yield), .groups = "drop")

# Select top 10 genotypes for visualization
top_genotypes <- met_means %>%
  group_by(genotype) %>%
  summarise(overall_mean = mean(mean_yield), .groups = "drop") %>%
  arrange(desc(overall_mean)) %>%
  head(10) %>%
  pull(genotype)

met_means %>%
  filter(genotype %in% top_genotypes) %>%
  ggplot(aes(x = location, y = mean_yield, group = genotype, color = genotype)) +
  geom_line(linewidth = 1, alpha = 0.7) +
  geom_point(size = 3) +
  theme_minimal() +
  scale_color_viridis_d() +
  labs(
    title = "Genotype × Environment Interaction (Top 10 Genotypes)",
    x = "Location", 
    y = "Mean Yield (kg/ha)"
  )

Model Fitting

# Fit Multi-Environment Model
met_model_fixed <- mandala(
  fixed  = yield ~ genotype + location + genotype:location,
  random = ~ location:block,
  data   = met_data
)

summary(met_model_fixed)
var_comps_met <- summary(met_model_fixed)$varcomp
print(var_comps_met)

# Heritability Estimation
met_model_random <- mandala(
  fixed  = yield ~ location,
  random = ~ genotype + genotype:location + location:block,
  data   = met_data
)

h2_met <- h2_estimates(
  random_mod = met_model_random,
  fixed_mod  = met_model_fixed,
  genotype   = "genotype"
)
print(h2_met)

# BLUPs
blups_by_loc <- mandala_predict(met_model_random, classify_term = "genotype:location")
blups_overall <- mandala_predict(met_model_random, classify_term = "genotype")
head(blups_overall)

Summary

This tutorial demonstrated:

RCBD Analysis — Simple randomized complete block design
Alpha-Lattice Design — Incomplete block designs
Multi-Environment Trials — Analyzing GxE interactions

Next Steps

Session Information

sessionInfo()

R version 4.5.2 (2025-10-31)
Platform: aarch64-apple-darwin20
Running under: macOS Tahoe 26.1

Matrix products: default
BLAS:   /System/Library/Frameworks/Accelerate.framework/Versions/A/Frameworks/vecLib.framework/Versions/A/libBLAS.dylib 
LAPACK: /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRlapack.dylib;  LAPACK version 3.12.1

locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8

time zone: America/New_York
tzcode source: internal

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods   base     

other attached packages:
[1] tidyr_1.3.1   ggplot2_4.0.0 dplyr_1.1.4  

loaded via a namespace (and not attached):
 [1] vctrs_0.6.5        cli_3.6.5          knitr_1.50         rlang_1.1.6       
 [5] xfun_0.54          purrr_1.1.0        generics_0.1.4     S7_0.2.0          
 [9] jsonlite_2.0.0     labeling_0.4.3     glue_1.8.0         htmltools_0.5.8.1 
[13] scales_1.4.0       rmarkdown_2.30     grid_4.5.2         evaluate_1.0.5    
[17] tibble_3.3.0       fastmap_1.2.0      yaml_2.3.10        lifecycle_1.0.4   
[21] compiler_4.5.2     RColorBrewer_1.1-3 htmlwidgets_1.6.4  pkgconfig_2.0.3   
[25] farver_2.1.2       digest_0.6.37      viridisLite_0.4.2  R6_2.6.1          
[29] utf8_1.2.6         tidyselect_1.2.1   pillar_1.11.1      magrittr_2.0.4    
[33] withr_3.0.2        tools_4.5.2        gtable_0.3.6